Frecuencia de Muestreo - Otra perspectiva Diferente
- JuanS
- Mar 31, 2020
- 10 min read
Updated: Apr 14, 2020
La frecuencia de muestreo es uno de esos temas controversiales que quienes estamos involucrados en la industria del audio solemos discutir y debatir ferozmente. No es un concepto esencialmente complejo; sin embargo, sus ramificaciones son increíblemente extensas. Quizás debido a que estas sí llegan a ser complicadas, a menudo nos conformamos con aseveraciones simples que, si bien no podemos probar, soportan nuestra manera de pensar. Como era de esperarse en una discusión así entran siempre conceptos como el clásico Teorema de Nyquist y Shannon y el ancho de banda del oído. Seguramente, al momento de leer esto muchos tendrán fuertes posturas frente al tema y quizás hasta se hayan casado con algún paradigma de cómo escoger la frecuencia de muestreo óptima para diferentes circunstancias. Sin embargo, me gustaría compartir nuevamente una perspectiva diferente que no necesariamente les hará cambiar de opinión, pero sí apreciar el problema con mayores y mejores bases, entender un poco más allá de lo que comúnmente se conoce y quizás hasta estar abiertos a que no todo es tan blanco ni tan negro.
Muestreo 101
Conceptualmente, el muestreo no es algo difícil de entender. Ante una gran densidad de información tomamos algunos ejemplos o muestras representativas de la población a nuestra disposición para darnos una idea de cuál es el comportamiento generalizado de la misma. La intención de esto es simplemente hacer la información más manejable ante un conjunto de recursos y condiciones de operabilidad. Un muestreo ideal, no obstante, se caracteriza por permitir la recuperación completa de la información poblacional sólo a partir de las muestras, lo cual, lógicamente, no es nada fácil.
En audio, debido a que las señales analógicas son continuas, el muestreo es esencial para poder manipularlas en el dominio digital. Naturalmente, la regla más conocida para hacer eso efectivamente es el teorema de Nyquist-Shanon. Este indica que para muestrear correctamente una señal la misma debe tener un espectro con un ancho de banda menor a la mitad de la frecuencia de muestreo, conocida como frecuencia de Nyquist (Si hay interés en discutir la demostración matemática de por qué esto es cierto y ahondar en la intuición detrás del postulado háganmelo saber ;) ). Es interesante ver que muestrear una señal es equivalente a multiplicarla por un tren de impulsos como se muestra en la siguiente gráfica.
Dado que un producto de señales en el tiempo es la convolución de sus espectros, la señal muestreada tiene en realidad infinitas replicas del espectro. La reconstrucción es igual de sencilla ya que lo único que necesitamos es eliminar las réplicas, y para esto, es suficiente multiplicarlas por un espectro rectangular como se muestra en la siguiente gráfica. Dado que el producto de espectros es la convolución entre señales en el dominio del tiempo, la reconstrucción se puede realizar de manera perfecta como la convolución de una función sinc con nuestra señal muestreada como se muestra a continuación.
Debido a que el postulado anterior ha sido demostrado matemáticamente, la mayoría de las discusiones se centran en si el teorema es realizable en la práctica o sobre uno de los efectos de no cumplir las condiciones del teorema: el aliasing. Este ultimo ocurre cuando dos senoidales de diferentes frecuencias, tras ser muestreadas, arrojan exactamente el mismo conjunto de puntos. Se dice que una es un alias de la otra porque en el sistema digital son indistinguibles. Es natural que esto ocurra cuando muestreamos una señal si la misma no está correctamente limitada en banda, ya que la expansion espectral superpondrá los espectros replicados; sin embargo, es importante ver que el aliasing no es un fenómeno exclusivo del muestreo (más sobre esto después). Dudamos de la calidad de los filtros anti-alias de nuestra interfaz de audio pues, o bien deterioran nuestra señal o son incapaces de limitarla en banda de la manera correcta. Tenemos dudas y ¡está bien! Sin embargo, hay una historia oculta en este asunto que rara vez se ve en las discusiones.
Lo que no dice el teorema!
El teorema del muestreo nos indica que muestreando un conjunto de instantes limitados podemos reconstruir completamente nuestra señal. En esencia, es una receta para el almacenamiento eficiente de la información; sin embargo, ¡el teorema no promete nada acerca de qué ocurre si modificamos las muestras en el domino digital! Más aún, si bien ese conjunto de muestras reconstruirán la señal, no por esto son una buena representación de la forma de onda analógica que muestrearon. Las siguientes dos gráficas muestran un par de señales digitales, intentemos predecir las formas de onda analógicas que generarán.
¿Coincide con lo que esperabamos? Es precisamente por esto que el teorema funciona, porque habiendo infinitas maneras de conectar las muestras, hay una y sólo una combinación de senoidales inferiores a la frecuencia de Nyquist que pasan por todos estos puntos, de hecho conectarlas de cualquier otra manera implicaría que nuestra señal ya no estaría limitada por la frecuencia de Nyquist. (Noten que técnicamente esto también permite el muestreo de señales limitadas en banda más no necesariamente con espectros en la banda base, entre -fs/2 y fs/2!).
Una perspectiva diferente
Ya que tenemos las herramientas suficientes, ahora sí me gustaría compartirles una perspectiva diferente. Los sistemas digitales y en general los lenguajes de programación rara vez tienen un concepto concreto y definido del tiempo y al no entenderlo, tampoco tiene una noción de lo que son las frecuencias en Hertz (unidades recíprocas al tiempo 1/s). Por esta razón, se fían de que nosotros les indiquemos cuál es al frecuencia de muestreo para escalar toda su maquinaria algorítmica y producir un resultado sensato en el dominio analógico. La frecuencia de muestreo, desde el punto de vista digital, es lo que permite al computador saber que tan rápido reproducir la información cuando queremos escucharla, saber cuántas muestras generar si requerimos una longitud precisa de material o por cuántas muestras debe extender una señal para simular una reverberación de un tiempo determinado. En esencia, este parámetro toca todos y cada uno de nuestros procesadores y lo obliga a reinterpretar lo que significa tener una muestra detrás de otra para seguir generando el mismo resultado temporal.
Por ejemplo, un ciclo de una onda senoidal de 441Hz se ve idéntica a un ciclo de una onda senoidal de 480Hz cuando la primera se genera en un sistema a 44.1kHz y la segunda en un sistema con una frecuencia de muestreo a 48kHz.
Naturalmente esto nos lleva a pensar que un filtro de rechazo de banda (“Notch filter”) a 441Hz a una frecuencia de muestreo de 44.1kHz es exactamente el mismo algoritmo que el mismo tipo de filtro en 480Hz a 48kHz y por consiguiente filtrar 480Hz es diferente a 44.1kHz que a 48kHz. Todos y cada uno de nuestros algoritmos, cada plug-in, cada fade, cada automatización, cada manipulación de la señal que utilice de manera alguna el tiempo o la frecuencia cambiará su definición al cambiar la frecuencia de muestreo; y aunque en la mayoría de los casos hay los resultados son idénticos, es sorprendente que los casos en los que no son relativamente poco conocidos.
Aliasing digital
Un error común es pensar que el aliasing es un posible daño colateral de la digitalización pero en realidad es una característica de cualquier sistema discreto. El mismo ocurre cuando el espectro se expande más allá del ancho de banda delimitado por la frecuencia de Nyquist. Debido a esto, cualquier proceso no lineal (cuya característica esencial, en este caso, es que produce más contenido espectral que el de la señal previa al proceso) puede, potencialmente, generar aliasing. Debido a que el aliasing está directamente relacionado con la frecuencia de Nyquist y con la frecuencia de muestreo, el comportamiento de estos procesadores puede cambiar drásticamente al cambiar la frecuencia de muestreo.
El caso más sencillo para evidenciar esto es la aplicación de un proceso de distorsión invariable en el tiempo, por ejemplo elevar la señal al cuadrado. Este proceso es particularmente fácil de entender en el dominio del tiempo como en el de la frecuencia, por lo que servirá perfectamente a este propósito. Elevar una señal al cuadrado es en esencia multiplicarla por sí misma por lo que, en el dominio de la frecuencia, es equivalente a una auto-convolución (una convolución de un espectro con sí mismo).
Adicionalmente, debido a simples identidades trigonométricas sabemos que cos(x)^2 = (1 + cos(2x))/2, por lo que sabemos, que a lo más, la mayor frecuencia llegará al doble de la mayor frecuencia existente.
Si este nuevo contenido espectral cayera por encima de la frecuencia de Nyquist diríamos que se convierte en un alias de una frecuencia por debajo de dicho limite. La siguiente gráfica muestra este proceso.
Naturalmente, este no es el comportamiento ideal por lo que es común implementar algún tipo de sobremuestreo interno en el procesador para evitar el aliasing. No obstante, esto tiene un costo computacional y otras varias afecciones sobre la señal misma que valdría la pena considerar. El sobremuestreo implica el uso de filtros anti-alias adicionales que incrementan la complejidad del proceso y dan paso a un nuevo conjunto de problemas adicionales. ¿Qué filtros se usan? ¿Cómo afectan la fase? ¿Cómo modifican la latencia? ¿están todos y cada uno de los pasos involucrados correctamente implementados?
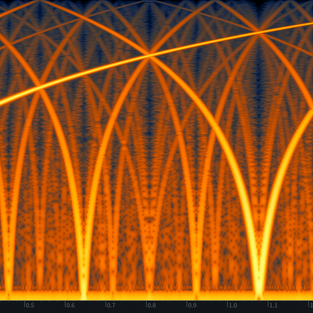
Las siguientes gráficas muestran una barrido de frecuencias de un procesador de distorsión a tres frecuencias de muestreo diferentes.
Adicionalmente, los siguientes audios evidencian que este no es un asunto imperceptible.
Finalmente, no crean que esto es poco común o exclusivo de la distorsión. Ciertamente en la distorsión es donde es más difícil de controlar pues la expansión espectral puede ser bastante agresiva. Esto sin mencionar que a menudo un fabricante debe favorecer la simplicidad del diseño para obtener un procesador con una latencia menor y hacer que el mismo sea utilizable en el contexto de grabación (e.g. simuladores de distorsión para guitarra) y por esto, quizás, aun entendiendo todo lo que implica, pueden optar por aceptar la posibilidad de algo de aliasing en pro de que el producto sea utilizable en una sesión de grabación, por ejemplo.
Deformación del eje de frecuencias en filtros IIR.
Los filtros analógicos tipo IIR (respuesta impulso infinita por sus siglas en inglés Infinite Impulse Response) se basan en la suma directa y retroalimentada de diferentes derivadas de una señal. Sin embargo, en el dominio digital, las derivadas, y en general todo lo que tiene que ver con el cálculo y el uso del concepto del infinitesimal esta restringido por la frecuencia de muestreo. Para una frecuencia baja, tomar la pendiente entre dos puntos contiguos en una señal puede funcionar bien ya que la velocidad a la que varía la señal es baja, pero en frecuencias altas la separación entre muestras (el periodo de muestreo) junto con la frecuencia de la señal no permiten una buena aproximación a la pendiente de la señal en ese punto. Debido a esto la digitalización de un filtro analógico tiene algunas complicaciones que pueden o no verse afectadas por la frecuencia de muestreo. Si bien existen métodos numéricos, como el método de euler, para calcular las derivadas y estos de hecho se utilizan para digitalizar ciertos procesos, el método más común para realizar este proceso es la transformada Bilineal o método de Tunstin o método del trapecio (Avísenme si hay interés en mirar este tema a mayor profundidad). Conceptualmente, permite la conversión de una función de transferencia analógica en una digital con ventajas como la preservación del orden de los filtros, la preservación de la complejidad de su modelo de polos y zeros y la certeza de obtener un filtro estable (Noten que cualquier sistema que utilice retroalimentación puede volverse inestable si se configura de manera incorrecta). Para lograr esto, toma el eje de frecuencias analógico, que es esencialmente infinito en extensión, y lo contrae y acomoda en el rango entre 0 y fs/2. Por supuesto que esto va a deformar el eje de frecuencias! Por lo que la transformada bilineal permite un parámetro adicional para hacer que una y sólo una frecuencia analógica coincida con una frecuencia digital. Usualmente este último parámetro se utiliza para obtener exactamente la misma fase y magnitud entre el filtro digital y el analógico en la frecuencia central del filtro, pero esto deja a todas las otras frecuencias vulnerables al efecto de la deformación. La siguiente gráfica muestra cómo se realiza esta deformación del eje de frecuencias
Y esta muestra varios ejemplos de filtros digitales creados con transformadas bilineales junto con sus contrapartes analógicas para evidenciar cómo la deformación del eje de frecuencias afecta sus funciones de transferencia.
Noten que la deformación tiene efecto notable solamente en las frecuencias altas y en mayor proximidad a la frecuencia de Nyquist, debido a esto es lógico pensar que el efecto de esta deformación será menor con una frecuencia de muestreo más alta. Por ejemplo un filtro paramétrico en 10kHz tendrá la misma deformación frecuencial a 48kHz que un filtro en 20kHz cuando la frecuencia de muestreo está en 96kHz. Nuevamente, para el algoritmo la frecuencia de muestreo representa la velocidad a la que se reproducirán las muestras, y por tanto lo que es relevante es la frecuencia del filtro en relación con la frecuencia de muestreo. Debido a esto la mayoría de la literatura de filtros digitales usa ejes de frecuencia normalizados en donde fs corresponde a 1. En el caso anterior un filtro en 10kHz a 48kHz esta en una frecuencia normalizada de 0.21Hz/fs justo al igual que uno a 20kHz cuando la frecuencia de muestreo es 96kHz. Estos dos filtros, algoritmicamente, no sólo son similares, ¡son idénticos!.
Pareciera entonces que la solución podría ser el sobremuestreo interno nuevamente; sin embargo, dado que en el caso de un sistema lineal no hay una expansión espectral esto puede ser ineficiente ya que el espectro adicional no es realmente necesario. Adicionalmente existen otros métodos para mejorar la transformada bilineal y obtener una función de transferencia en donde el comportamiento de la deformación frecuencial sea el adecuado (De hecho yo escribí un paper atacando precisamente este punto de una manera diferente ;) ).
Algunas ideas finales
El procesamiento digital de señales es un campo increíblemente rico en posibilidades, y así mismo, cada una de ellas viene con sus propios problemas y soluciones, pero en cada caso, la frecuencia de muestreo es una variable que indudablemente puede afectar el desempeño de los algoritmos utilizados. Quería compartirles dos problemáticas que considero son relativamente fáciles de entender y que a su vez tienen gran impacto sobre la realidad práctica del audio por lo que es relativamente fácil ponerlos en evidencia. Sin embargo, sepan que ¡hay una infinidad más! La variabilidad de la longitud de los filtros FIR y cómo esto afecta la latencia, la dependencia de la precisión de los coeficientes de los filtros recursivos (IIR) con la frecuencia de muestreo, la variabilidad del comportamiento de filtros dentro de reverberaciones, flangers y phasers, la precisión en mediciones relacionadas con la forma de onda, la distorsión por intermodulación de contenido espectral inaudible y muchas cosas más; TODAS relacionadas y afectadas por la frecuencia de muestreo. Ciertamente hay conversaciones interesantes a propósito de la calidad de los filtros anti-alias en CADs (convertidores de análogo a digital) pero con todo lo que pasa en el mundo digital, que no está para nada explicado por el Teorema de Nyquist-Shannon, realmente creemos que ese tiene que seguir siendo el único argumento relevante a la hora de discutir ¿qué es la frecuencia de muestreo?
Personalmente, creo que he cambiado de postura frente al tema tantas veces como es posible. Empecé aferrándome a ciertas ideas pero a menudo que estudiaba las revaluaba y terminaba “cambiándome de bando”, estudiaba un poco más y volvía a mi postura inicial y entre más información tenía más me daba cuenta de una realidad que considero aplicable a cualquier situación similar: Cuando algo genera tanta discusión la postura más ilógica es creer que la respuesta es evidente. Ciertamente es fácil encontrar personas de mucha experiencia y conocimiento en ambos lados de la discusión. 44.1 vs 192kHz es algo que ciertamente no se puede reducir a una obviedad. Son tantos los detalles que hay que considerar que es difícil argüir que mi postura o la de cualquier es evidentemente superior. Habiendo dicho esto, ¿qué piensan uds?









Comments